Ist die Natur wirklich so seltsam, wie die Quantentheorie sagt – oder gibt es doch anschaulichere Erklärungen? Neutronen-Messungen der TU Wien beweisen: Ohne Quantentheorie geht es nicht. Eine Presseaussendung der Technischen Universität Wien.
Quelle: Technische Universität Wien 1. Juli 2024.
1. Juli 2024 – Kann sich ein Teilchen an zwei unterschiedlichen Orten gleichzeitig aufhalten? In der Quantenphysik ist das kein Problem: Sie erlaubt, dass sich Objekte in verschiedenen Zuständen gleichzeitig befinden – oder präziser gesagt: In einem Überlagerungszustand, der sich aus unterschiedlichen beobachtbaren Zuständen zusammensetzt. Aber ist das wirklich der Fall? Vielleicht befindet sich das Teilchen in Wirklichkeit sehr wohl in einem ganz bestimmten Zustand, an einem ganz bestimmten Ort, nur kennen wir ihn nicht?
Seit Jahrzehnten wird über die Frage diskutiert, ob man das Verhalten von Quantenobjekten nicht vielleicht doch durch eine für uns anschaulichere Theorie beschreiben kann. 1985 wurde eine Möglichkeit vorgeschlagen, das zu messen – die sogenannte „Leggett-Garg-Ungleichung“. Jede Theorie, die ohne die merkwürdigen Überlagerungs-Zustände der Quantentheorie auskommt, muss dieser Ungleichung gehorchen. Die Quantentheorie hingegen verstößt gegen sie. An der TU Wien wurden dazu nun erstmals Messungen mit Neutronen durchgeführt – mit einem eindeutigen Ergebnis: Die Leggett-Garg-Ungleichung wird verletzt, klassische Erklärungen dafür sind nicht möglich, die Quantentheorie gewinnt. Die Ergebnisse wurden nun im Fachjournal „Physical Review Letters“ publiziert.
Physikalischer Realismus
Wir gehen normalerweise davon aus, dass jedes Objekt bestimmte Eigenschaften hat: Ein Ball befindet sich an einem bestimmten Ort, er hat eine bestimmte Geschwindigkeit, vielleicht auch eine bestimmte Drehung. Ob wir den Ball beobachten oder nicht, ist egal. Er hat diese Eigenschaften ganz objektiv und unabhängig von uns. „Diese Sichtweise wird als ‚Realismus‘ bezeichnet“, sagt Stephan Sponar vom Atominstitut der TU Wien.
Insbesondere große, makroskopische Objekte müssen dieser Regel gehorchen, das wissen wir aus unserer Alltagserfahrung. Außerdem wissen wir: Makroskopische Objekte kann man beobachten, ohne sie nennenswert zu beeinflussen. Die Messung ändert den Zustand nicht. Diese Annahmen bezeichnet man zusammen als „makroskopischen Realismus“.
Die Quantentheorie, wie man sie heute kennt, ist aber eine Theorie, die diesen makroskopischen Realismus verletzt. Wenn für ein Quantenteilchen unterschiedliche Zustände erlaubt sind, zum Beispiel unterschiedliche Positionen, Geschwindigkeiten oder Energiewerte, dann ist auch eine beliebige Kombination dieser Zustände erlaubt. Zumindest, solange man diesen Zustand nicht misst. Bei einer Messung geht dieser Überlagerungszustand nämlich kaputt: Die Messung zwingt das Teilchen, sich für einen ganz bestimmten Wert zu entscheiden.
Die Leggett-Garg-Ungleichung
Trotzdem muss die Quantenwelt mit der makroskopischen Welt logisch zusammenhängen – schließlich bestehen große Dinge ja aus kleinen Quantenteilchen. Prinzipiell sollten die Regeln der Quantentheorie für alles gelten.
Die Frage ist nun also: Kann man bei „großen“ Objekten ein Verhalten finden, das sich mit unserem intuitiven Bild des makroskopischen Realismus nicht vereinbaren lässt? Können auch makroskopische Dinge klare Anzeichen von Quanteneigenschaften aufweisen?
1985 veröffentlichten die Physiker Anthony James Leggett und Anupam Garg eine Formel, mit der sich der makroskopische Realismus testen lässt: Die Leggett-Garg-Ungleichung. „Der Gedanke dahinter ist ähnlich wie bei der berühmteren Bell’schen Ungleichung, für deren Überprüfung 2022 der Physik-Nobelpreis vergeben wurde“, sagt Elisabeth Kreuzgruber, Erstautorin des Papers. „Allerdings geht es bei der Bell’schen Ungleichung um die Frage, wie stark das Verhalten eines Teilchens mit einem anderen, quantenverschränkten Teilchen zusammenhängt. Bei der Leggett-Garg-Ungleichung geht es nur um ein einziges Objekt, und um die Frage, wie sein Zustand zu bestimmten Zeitpunkten mit seinem Zustand zu anderen Zeitpunkten zusammenhängt.“
Stärkere Korrelationen als die klassische Physik erlaubt
Leggett und Garg gingen von einem Objekt aus, das zu drei verschiedenen Zeitpunkten gemessen werden kann, jede Messung kann zwei verschiedene Ergebnisse haben. Auch wenn man überhaupt nichts darüber weiß, ob oder wie sich der Zustand dieses Objekts im Lauf der Zeit ändert, kann man trotzdem statistisch untersuchen, wie stark die Ergebnisse zu unterschiedlichen Zeitpunkten miteinander zusammenhängen.
Man kann mathematisch zeigen, dass die Stärke dieser Zusammenhänge ein gewisses Maß niemals übersteigen kann – wenn man voraussetzt, dass der makroskopische Realismus korrekt ist. Leggett und Garg konnten eine Ungleichung aufstellen, die von jeder makroskopisch realistischen Theorie immer erfüllt sein muss, ganz egal um welche Theorie es sich im Detail handelt.
Wenn sich das Objekt allerdings an die Regeln der Quantentheorie hält, dann müssen sich deutlich stärkere statistische Zusammenhänge zwischen den Messergebnissen zu den drei verschiedenen Zeitpunkten ergeben. Wenn ein Objekt sich zwischen den Mess-Zeitpunkten tatsächlich in verschiedenen Zuständen gleichzeitig befindet, muss sich das – nach Leggett und Garg – in stärkeren Korrelationen zwischen den drei Messzeitpunkten zeigen.
Neutronenstrahlen: Zentimetergroße Quantenobjekte
„Allerdings ist es gar nicht so einfach, diese Frage experimentell zu untersuchen“, sagt Richard Wagner. „Wenn wir den makroskopischen Realismus testen wollen, dann brauchen wir ein Objekt, das in gewissem Sinn makroskopisch ist, das also eine Größe hat, die mit der Größe unserer gewohnten Alltagsgegenstände vergleichbar ist.“ Gleichzeitig muss es sich aber um ein Objekt handeln, bei dem man eine Chance hat, Quanten-Eigenschaften zu erkennen.
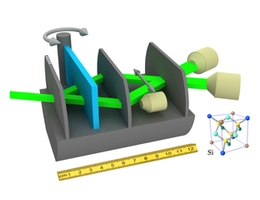
„Neutronenstrahlen, wie wir sie in einem sogenannten Neutroneninterferometer vorfinden, sind dafür perfekt“, sagt Hartmut Lemmel, Strahlplatzverantwortlicher am Instrument S18 des Institut Laue-Langevin (ILL) in Grenoble, wo das Experiment durchgeführt wurde. Im Neutroneninterferometer, einem Silizium-Perfektkristall-Interferometer, das in den frühen 1970er Jahren am Atominstitut der TU Wien erstmals erfolgreich zum Einsatz kam, wird der einfallende Neutronenstrahl an der ersten Kristallplatte in zwei Teilstrahlen aufgespalten und danach von einem weiteren Silizium-Stück wieder zusammengeführt. Es gibt somit zwei verschiedene Wege, auf denen Neutronen von der Quelle zum Detektor gelangen können.
„Die Quantentheorie sagt: Jedes einzelne Neutron nimmt beide Wege gleichzeitig“, sagt Niels Geerits. „Die beiden Teilstrahlen sind aber mehrere Zentimeter voneinander entfernt. In gewissem Sinn hat man es hier also mit einem Quantenobjekt zu tun, das eine für Quanten-Verhältnisse gewaltige Größe hat.“
Durch eine ausgeklügelte Kombination mehrerer Neutronenmessungen konnte das Team der TU Wien die Leggett-Garg-Ungleichung testen – und das Ergebnis war eindeutig: Die Ungleichung wird verletzt. Die Neutronen benehmen sich also auf eine Weise, die mit keiner erdenklichen makroskopisch realistischen Theorie erklärt werden kann. Sie befinden sich tatsächlich auf beiden Strahlen gleichzeitig, an unterschiedlichen Stellen, die Zentimeter auseinanderliegen. Die Idee „vielleicht bewegt sich das Neutron doch nur auf einer der beiden Bahnen, wir wissen bloß nicht welche“ ist damit widerlegt.
„Unser Experiment zeigt: Die Natur ist tatsächlich so seltsam, wie die Quantentheorie behauptet“, sagt Stephan Sponar. „Egal welche klassische, makroskopisch realistische Theorie man sich zurechtlegt: Sie wird die Wirklichkeit niemals erklären können. Ohne Quantenphysik geht es nicht.“
Originalpublikation
E. Kreuzgruber et al., Violation of a Leggett-Garg Inequality Using Ideal Negative Measurements in Neutron Interferometry, Phys. Rev. Lett. 132, 260201 (2024).
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.132.260201
Diskutieren Sie mit im Raumcon-Forum: